ベース接地回路は、私にとって動作イメージが「一番わかりにくかった」増幅回路です
図などを使い、ベース接地回路の「特徴と動作イメージ」をわかりやすく解説したいと思います
他のトランジスタ増幅回路は、こちらに記事があります
オームの法則について、こちらの記事が詳しいです

ベース接地回路とは
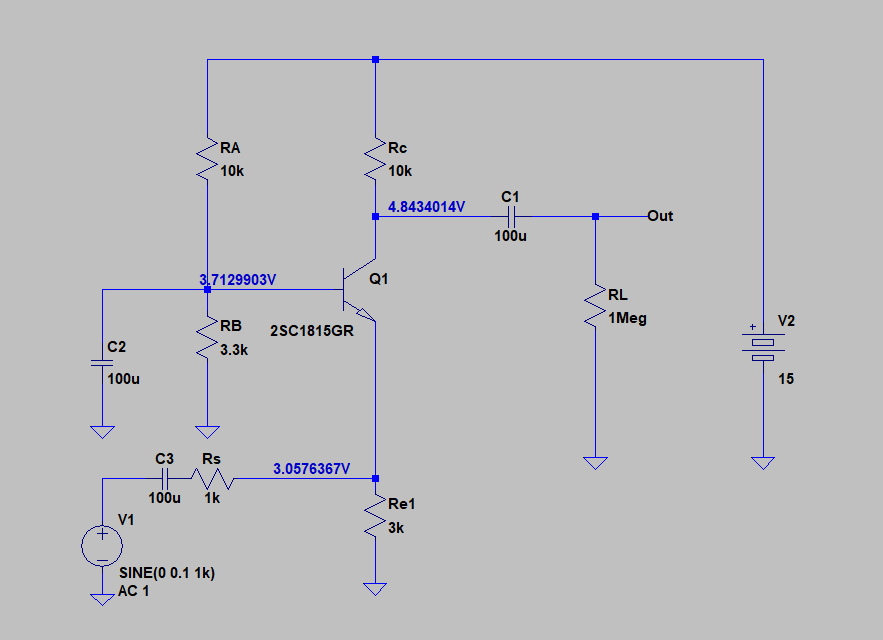
ベース接地回路は、高周波回路でよく使われます
逆に言えば、低周波増幅で単体で使われることは稀です
それは、ベース接地回路が「こんな特徴」をもっているからです
- トランジスタのベース端子を共有(共通)した増幅回路
- 入力と出力は同じ波形(同相)
- 電圧利得: (Rc//RL)/Rs
- 電流利得:1倍より小さい
- 入力インピーダンスが「とても小さい」
- 出力インピーダンスが「大きい」
- 高周波特性がエミッター接地回路より優れている
ベース接地回路の「特徴と動作イメージ」
あまり難しいことは、専門書に任せるとして
特徴と動作イメージを見てみましょう
ベースは交流的に共有(接地)
ベース接地回路は、このようにベースが共有されています
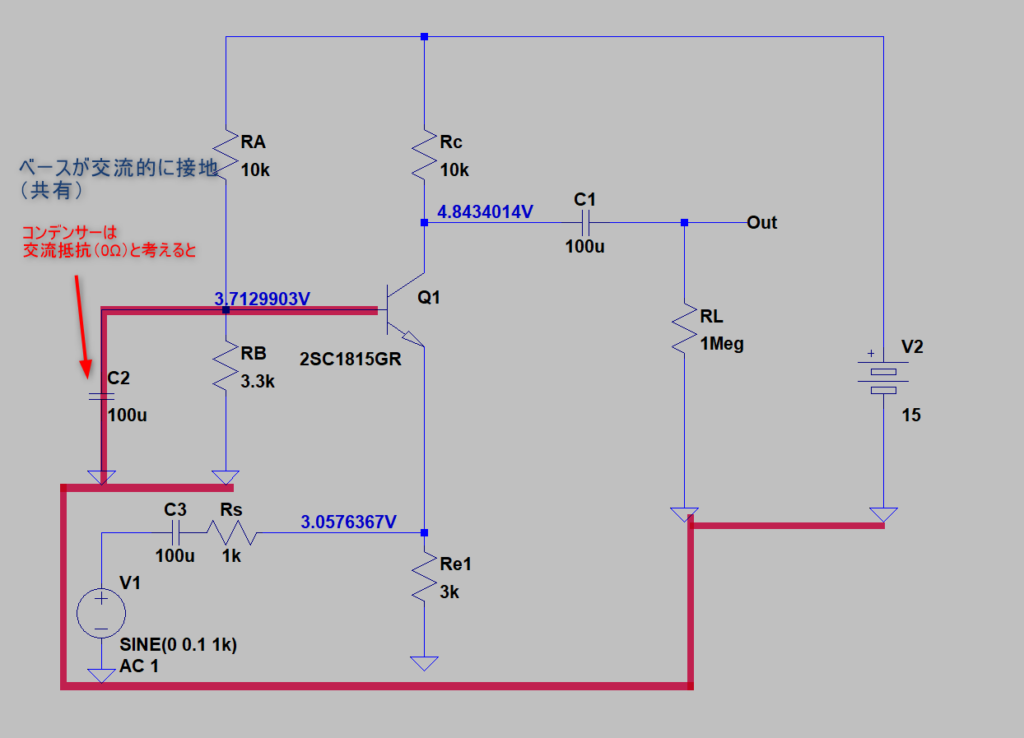
コンデンサーは交流的に見れば、ショート(0Ω)と同じです
ベース接地回路では
- 入力はエミッタです(正確にはベース/エミッタ間)
- 出力はコレクタです(V2-Vc)
ということは・・・
入力は図の通り「エミッタ」です
そして、エミッタは定電圧動作です
定電圧動作≒0Ωですから
ベース接地回路の「入力インピーダンスはとても小さい」
出力はエミッタ接地回路と同じですから
ベース接地回路の出力インピーダンスはエミッタ接地回路と同じ
Rc//RL・・・大きい
といえます
トランジスタの「コレクタとエミッタの違い」は、こちらに詳しく書いています

ベース接地回路の動作イメージ
ベース接地回路がどのように動作するか、イメージしてみましょう
筆者は最初、これがわかりませんでした・・・
まず、前提として
- エミッタは、完全な定電圧動作・・・トランジスタの入力抵抗は0Ω
- Ie=Ic
とします
理解のポイントは「抵抗Rs」を入れて考えるということです
Rsが無いと、入力電圧が変化してもRe1両端の電圧は変化しないため、
次はどこが変化して行くのか、迷子になります
それでは、入力電圧が上下した場合、
それぞれ順を追って見ていきましょう
入力が無い(0V)時の動作を確認

最初に、各電位を確認しましょう
- Rs両端には3V(Re1と同じ)の電圧がかかっています
- Rsに電位差が無いので、Iin=0です
- Re1を流れる電流は1mA「エミッタが定電圧」なので常に一定です
- Ieも1mAになります
- Ie=Icから、Ic=1mAです
- Icが1mA、Rc(10KΩ)によって電圧変化に変えられます
出力電位Voutは(V2-Vc)
=(15V-(1mAx10KΩ))=5V
出力電位5Vで、コンデンサーで直流カットされますから
交流出力は0Vです
入力電圧が0.1V上昇した場合
入力電圧が+0.1V変化しました・・・すると

- Rsに0.1Vの電圧が印加されます
- Rsに0.1mAの電流が「エミッタ向き」に流れます
- Re1を流れる電流は「エミッタが定電圧」なので常に一定です
- よって、Rs電流は「全てIeの変化(0.1mA減少)」になります
- Ie=Icから、Rs電流は「そっくりIcの変化(0.1mA減少)」です
- Icが1mA→0.9mAになり、Rcによって電圧変化に変えられます
出力電位は5V→6V(15-9=6)に変化します
交流出力は変化分ですから、(+1V)です
もう少し、詳しく見ていきましょう
①で印加された電圧(+0.1V)は、コンデンサーを通ってRsの入力側電圧を押し上げます
②Rsの入力側が3.1V、エミッタ側は定電圧ですから3Vです
オームの法則に従い、0.1V/1KΩ=0.1mAの電流(Iin)がエミッタ向きに流れます
③Iin(0.1mA)は、エミッタ電流(Ie)と合流してRe1を流れます
この時・・・
- エミッタ=定電圧
- Re1に掛かる電圧も一定
- Re1の電流は常に一定(Ve/Re1)です
- しかし、Iin(0.1mA)は合流してRe1を流れます
- その辻褄を合わせるため、トランジスタのIeが減少(-0.1mA)
④つまり、Iinの変化はそっくりIeの変化になります
⑤Ie≒Icです、今はIe=Ieと考えれば
Iinの変化はIcの変化です
⑥Icが0.1mA減少します
出力電位は(V2-Vc)ですから、Icが減り、Vcが減ると
出力電位は上昇して5Vから6Vになります
コンデンサーで直流カットされた、変化分(+1V)が出力電圧です
入力電圧が0.1V減少した場合
それでは、逆向きの変化も見てみます

入力電圧が(-0.1V)変化しました・・・すると
- Rsにー0.1Vの電圧が印加されます
- Rsに0.1mAの電流が「入力向き」に流れます
- Re1を流れる電流は「エミッタが定電圧」なので常に一定です
- よって、Rsの電流は「全てIeの変化(0.1mA増加)」になります
- Ie=Icから、Rs電流は「そっくりIcの変化(0.1mA増加)」です
- Icが1mA→1.1mAになり、Rcによって電圧変化に変えられます
出力電位は5V→4V(15-11=4)に変化します
出力電圧は変化分(-1V)です
ベース接地回路のゲイン

正確には
- Ic=(hfe/(1+hfe))xIe
- エミッタの電圧がIeの変化で変わる(トランジスタの入力インピーダンス)
などの理由で若干異なりますが
電子工作などでの「実用的な範囲」として電圧利得(ゲイン)は・・・
電圧利得(ゲイン)は、
入力電圧と出力電圧の変化分です
⊿Vout/⊿Vin
⊿Vout=⊿Icx(Rc//RL)
⊿Vin=⊿IinxRs
ここで、⊿Iin=⊿Ie=⊿Ic、RL>>Rcとすれば
⊿Vout=⊿IcxRc
⊿Vin=⊿IcxRsですから
ベース接地回路の電圧利得(ゲイン)は
⊿Vout/⊿Vin ≒ Rc/Rs
となりますね
※「RL>>Rc」は、RLがRcより十分に大きい
※「//」は抵抗の並列和です
この回路のゲインは、RLがとても大きいので
Rc/Rs=10倍、同相になりますね
「gm」や「hfe」といった、トランジスタの基本はこちらをどうぞ

ベース接地回路の強み=高周波特性が良い
エミッタ接地回路で、高周波ゲインが伸びない理由
なぜ、エミッタ接地回路は「周波数が高くなる」とゲインが低下するのでしょう
それは、トランジスタの各端子間に「コンデンサ」成分(寄生容量)があるからです
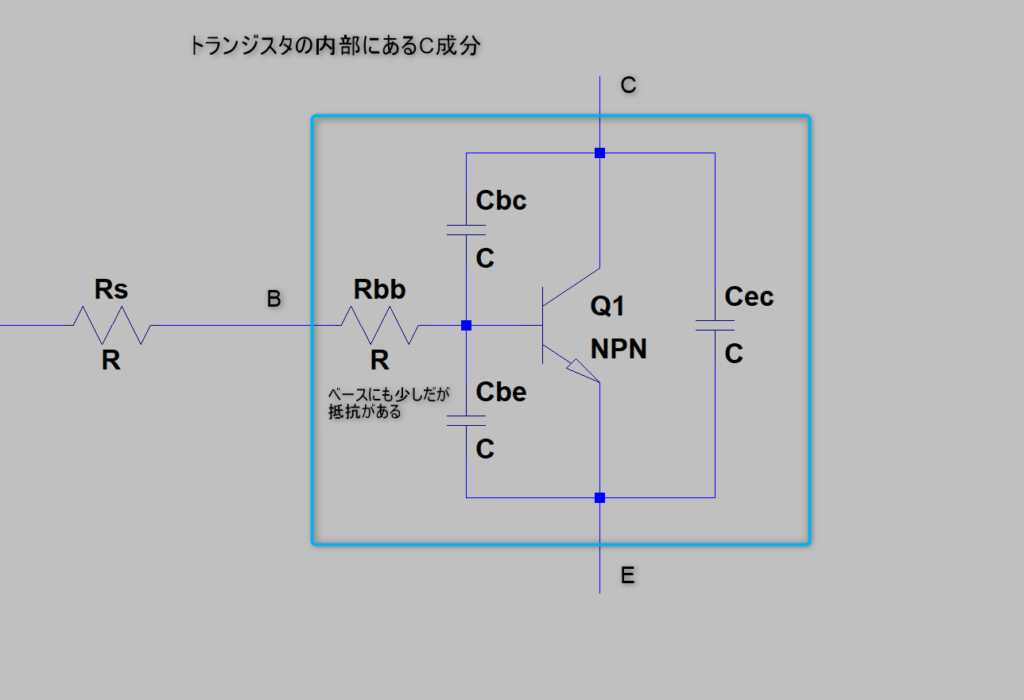
この「寄生容量」と「抵抗」によって入力に「ローパスフィルタ」が形成されます
ローパスフィルタとは、低い周波数を通過させ、高い周波数では減衰するフィルタです
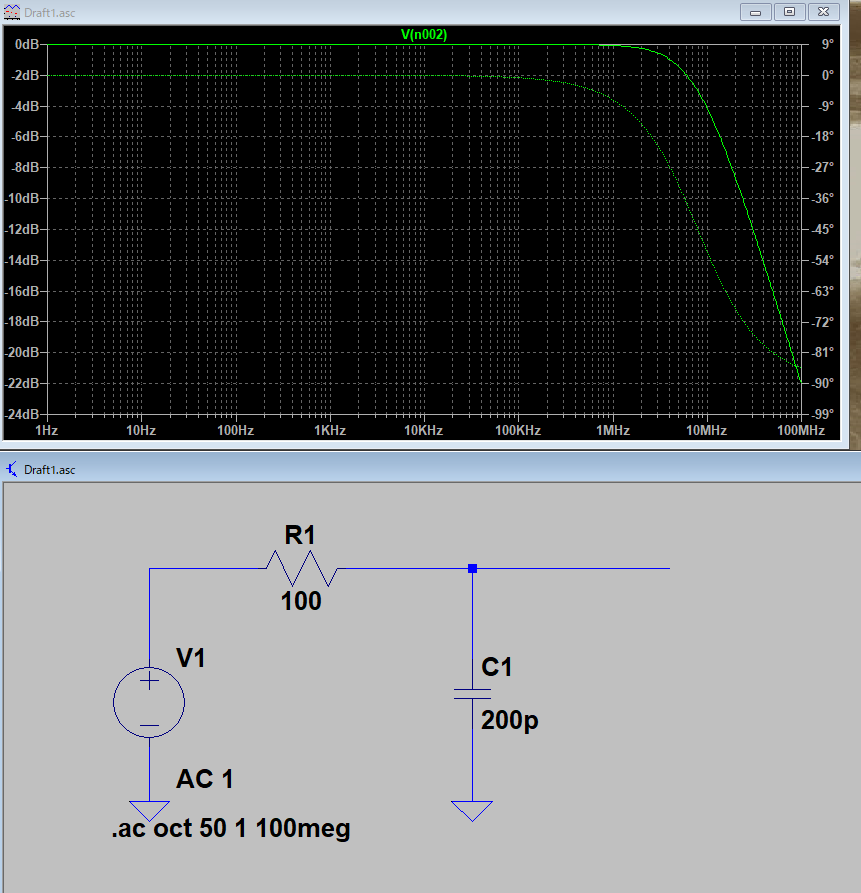
これが、高い周波数でゲインが低下する理由です
特に問題が大きいのが
エミッタ接地回路での「Cbc(ベース/コレクタ間の容量)」です
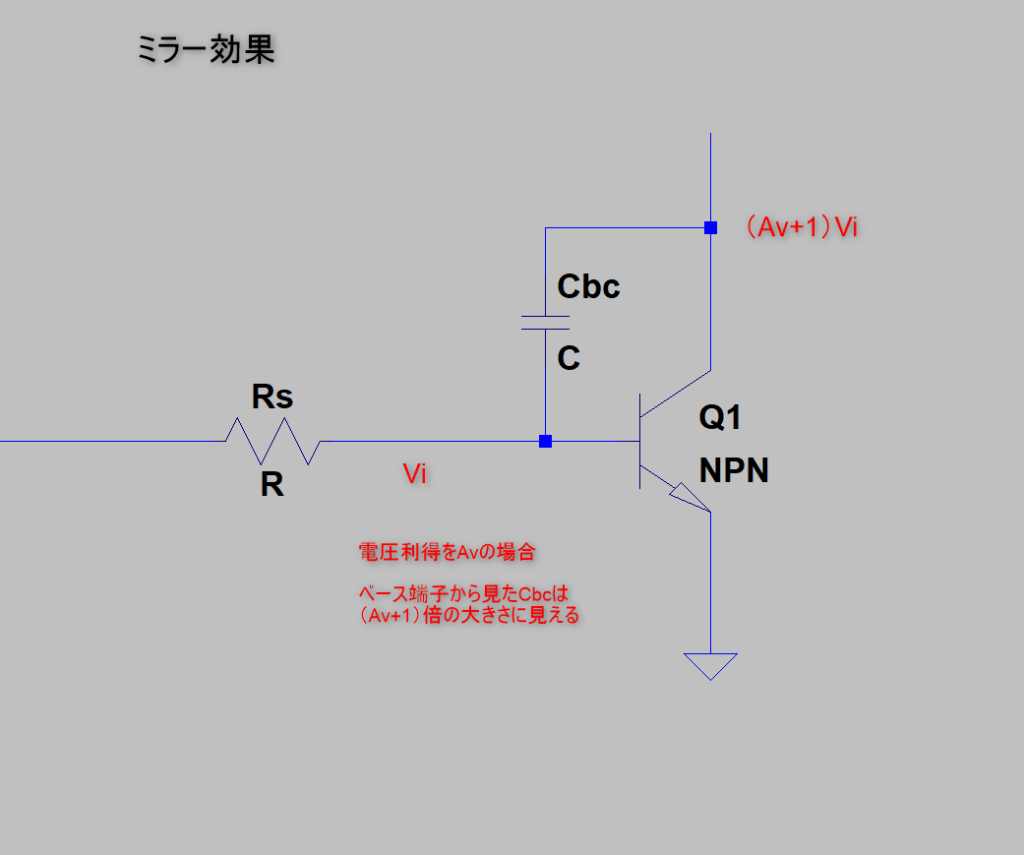
エミッタ接地回路では、ベースに入力電圧Vi
コレクタに(電圧利得=Av倍)の電圧(逆相)が印加されます
この時、Cbcの両端には
(Vi-(-VixAv))=(Av+1)Vi
Viの(Av+1)倍の電圧がかかります
つまり・・・エミッタ接地回路のベースからCbcを見ると
(Av+1)xCbc
のコンデンサに見えるのです
「ミラー効果」と呼ばれる現象です
エミッタ接地回路では
- 入力側の抵抗(Rsなど)
- (Av+1)倍されたCbc
の間で「ローパスフィルタ」が形成されます
そのため、エミッタ接地回路では、
高い周波数で利得を稼ぐことが難しいのです
ベース接地回路は「ミラー効果」の影響がない
ベース接地回路は、電圧利得(Av)があるにもかかわらず
ミラー効果の影響がありません
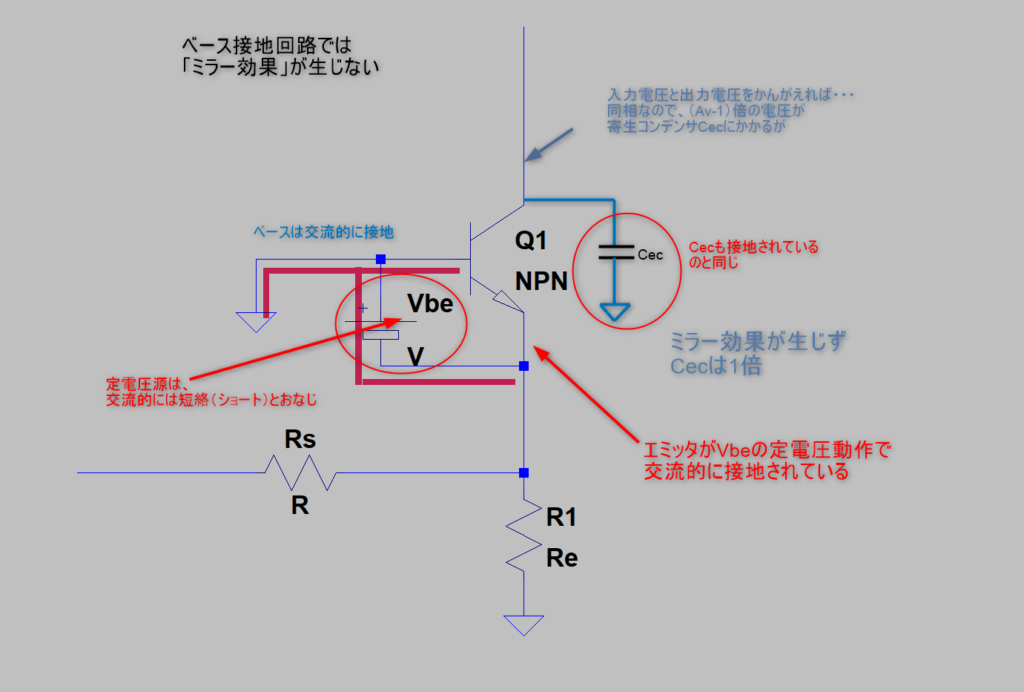
一見すると、エミッタとコレクタに(Av-1)倍の電圧がかかっています
普通に考えると入力側に「RsやRe」と(Av-1)倍(Cec)で「ローパスフィルタ」できそうに見えます・・・
しかし、ベース接地回路では、ミラー効果の影響がないのです
ベース接地回路ではエミッタに電圧振幅が現れません
- これは、エミッタが「定電圧動作」だからです
- ベース/エミッタ間を「定電圧源」とすれば
- 交流的にはベース/エミッタ間は「短絡(ショート)」と同じ
つまり、「エミッタは交流的に接地(GND)」とみなせます
「ローパスフィルタ」が形成されるのは、入力ーGND間に「コンデンサ」が入るためです
入力が接地されてしまえば、「ミラー効果」の影響が生じないわけです
まとめ
トランジスタの「ベース接地増幅回路」は・・・
- トランジスタのベース端子を共有(共通)した増幅回路
- 入力と出力は同じ波形(同相)
- 電圧利得: (Rc//RL)/Rs
- 電流利得:1倍より小さい
- 入力インピーダンスが「とても小さい」
- 出力インピーダンスが「大きい」
ベース接地回路のエミッタ(入力)は、交流的接地
- ミラー効果の影響を生じない
- 高周波特性がエミッター接地回路より優れている
ベース接地回路は「単体」では非常に使いにくい回路ですが
周波特性が良いため「高周波増幅」ではよく使われます
低周波でも、エミッタ接地回路と組合せた「カスコード回路」として使われます