オームの法則は、電気を学ぶ上で、避けては通れない公式です
「とにかく苦手」、「計算や使い方がよくわからない」
「いやあ~この式、見るだけで鳥肌が立つ」
という方も、いるでしょう・・・
ですが、大丈夫です!
順番に理解していきましょう
そんな方でも、理解できるよう「わかり易く」基本から解説します
もちろん、「初めて学ぶ」方や「学生さん」でもOKです
それでは、はじめましょう
「オームの法則」とは
難しいこと抜きに「一言」でいいますと
「電圧(E)、電流(I)、電気抵抗(R)」の関係を公式にしたものです
電気の分野では、「オームの法則(公式)なしでは、何も出来ない」くらい、
「超」がつくほど「重要な公式」です
オーム法則「公式」
E(V) = I(A) X R(Ω)
「抵抗」の両端にかかる「電圧(V)」は
「抵抗値(Ω)」と、流れる「電流(A)」を掛け算して求められる
I(A)= E(V) / R(Ω)
「抵抗」を流れる「電流(A)」は
抵抗両端にかかる「電圧(V)」を「抵抗値(Ω)」で割って求められる
R(Ω)= E(V) / I(A)
「抵抗値(Ω)」は、
抵抗両端にかかる「電圧(V)」を「電流(A)」で割って求められる
オームの法則の公式は
1つの抵抗で「電圧」、「電流」、「抵抗値」のうち
2つが判明していれば、残りの一つを計算で求められる
オームの法則「公式」の覚え方
オームの法則「第一関門」が、この「公式」を
「いかにして覚えるか」というわけなのですが・・・
※方法1.「E=IR」と「等号の性質」を使う
「オームの法則」というと「公式3つ」というイメージが強いですが
実は、「一つの公式」が姿を変えただけです
E=IR
Rを導く式・・・右辺のIがジャマ
両辺をIで割ってやる
E/I=IR/I=R→ R=E/I
Iを導く式・・・右辺のRがジャマ
両辺をRで割ってやる
E/R=IR/R=I→ I=E/R
※E=IRだけ覚えておけば、他の公式は計算で求められます
また、どの式からでも、全ての公式を導く事ができます
そこで、計算法を使って
- 「E=IR」だけ暗記
- 残りの2つは「等号の性質」で必要な時に求める
この方法は、ひねりも何もないですが
暗記量が一番少なくて済む方法です
いろんな「公式の暗記」に応用できます
電気の道へ進みたい方、電気の資格を目指す方は、
大変でも、この方法をマスターしたいものです
ただ、文系志望の学生さんには、向かないかもしれないですね
※方法2. ビジュアル的に覚える
よく見かける図なのですが、とても便利です
学生さんの試験対策には、コチラの方法が向いているかも
この「図」を「イメージとして覚える」という方法です
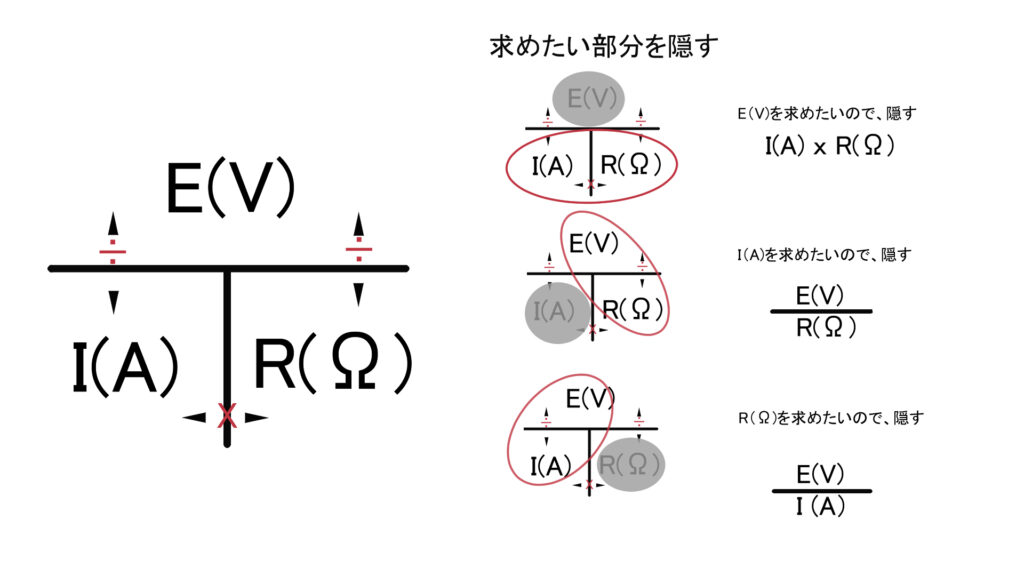
いろいろなバリエーションがあるようですが
使い方は、基本同じです
- まず、「求めたい文字」を隠す
- 残った文字が横並びなら「かける(x)」
- 残った文字が縦並びなら「分数(÷)」
- 「文字」に「値」を代入して計算すればOK
これは、解りやすいですね
この図を考えた方、すごくいい先生だと思います
※方法3. やっぱり気合で丸暗記する
人には、得手不得手があるものです
暗記が「メチャクチャ好き・得意」という方はいるもので
そんな能力をお持ちなら、「正攻法で丸暗記」というのもアリです
(学生の頃、有無を言わさず「3つ」覚えさせる先生、いましたね)
丸暗記にあたり
- E=IR以外の「公式2つ」は分数式
- 分数式の「分子(上側)」は、どちらも「E(V)」
こんなことを意識しておくと、良いでしょう
オームの法則、計算の基本
公式は「使ってナンボ」です
まずは、公式の使い方を「基本」から見ていきましょう
※電圧 (V)を求める(電圧がわからない)
E(V) = I(A)・R(Ω)
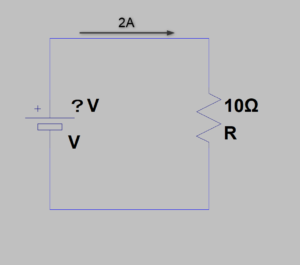
この回路のように
一つの抵抗の
電流、抵抗値がわかっていて
抵抗両端の電圧を求めたい場合
この公式を使います
公式に値を代入すると
E=2x10=20
答え:20V
※電流 I(A)を求める(電流がわからない)
I(A) = E(V) / R(Ω)
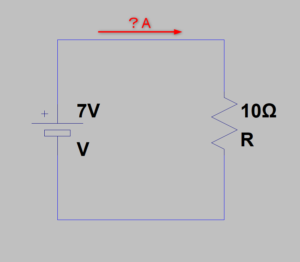
この回路のように
一つの抵抗の
電圧、抵抗値がわかっていて
抵抗を流れるの電流を求めたい場合
この公式を使います
公式に値を代入すると
I=7÷10=0.7
答え:0.7A(700mA)
※抵抗値 R(Ω)を求める(抵抗値がわからない)
R(Ω) = E(V) / I(A)
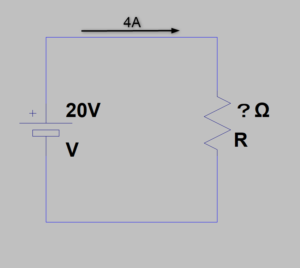
この回路のように
一つの抵抗の
電圧、電流がわかっていて
抵抗器の抵抗値を求めたい場合
この公式を使います
公式に値を代入すると
R=20÷4=5
答え:5Ω
オーム法則「公式」を使うときの注意
オームの法則が適用できるのは
どういうことかというと
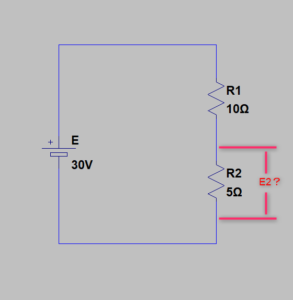
このような問題では
R2を流れる電流が不明です
まず、抵抗の合成などを使って
R2の電流を求めないと
いきなり「E2」は求められません
しかし、コチラの回路ならOK、求められます
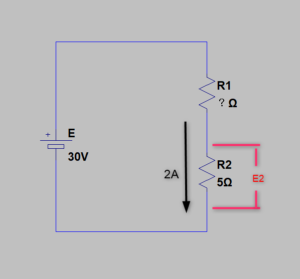
R1の抵抗値は不明でも
R2の電流、抵抗値が
わかっているからです
E2=R2xI=5x2=10
E2=10Vですね
(これ、テストならラッキー問題かも)
抵抗の合成
抵抗の合成(合成抵抗)は、
複数の抵抗を、あたかも「一つの抵抗に見える」ように
計算でまとめる方法です
合成すれば、見かけ上「1本」の抵抗のように扱えます
抵抗のつながり方は
- 直列接続
- 並列接続
のどちらかしかありません
※どんなに複雑に見えても、紐解いていけば、必ずこのどちらかになります
抵抗の直列接続
このように、「一列」につなぐことを「直列接続」といいます
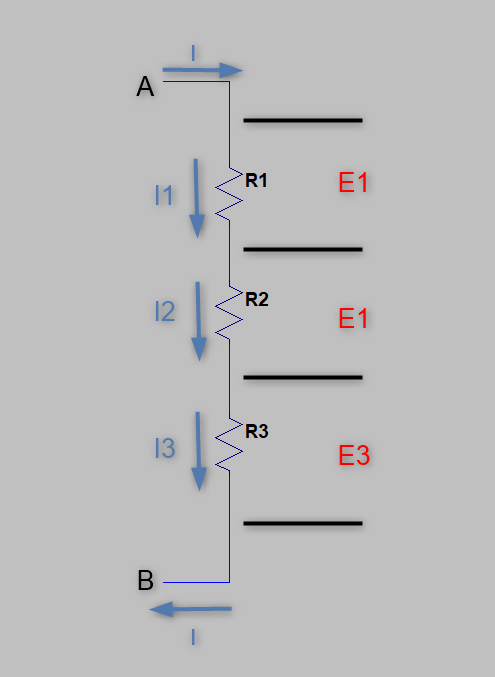
A-B間から見ると、電気的に「一つの抵抗」に見えます
A-B間の抵抗値を「R」とすると
R = R1 + R2 + R3
抵抗がR4、R5・・・と増えても同じように計算します
さて、これだけなら話は割と簡単なのですが
抵抗の直列接続に「特有の性質」を知っておく必要があります
「直列接続」を流れる「電流I」は「全て同じ値」
I=I1=I2=I3
A-B間の「電圧をE」とすれば、
各抵抗の両端電圧の関係は
- ① E=E1+E2+E3
- ② 各抵抗の電圧は「抵抗値の比」になる
- これは、R1:R2:R3 = E1:E2:E3 ですね
抵抗の直列回路を「実際に計算」してみる
この回路で「電流」と「電圧」をそれぞれ計算してみます
この計算では、直列抵抗の「合成抵抗」と「特有の性質」を使っています
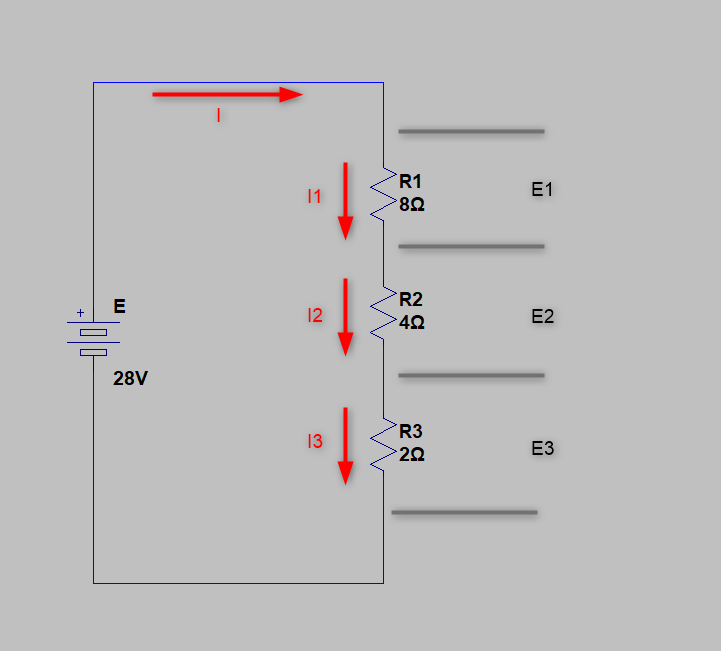
合成抵抗「R」と全電流「I」
まず、合成抵抗「R」と全体の電流「I」を求めます
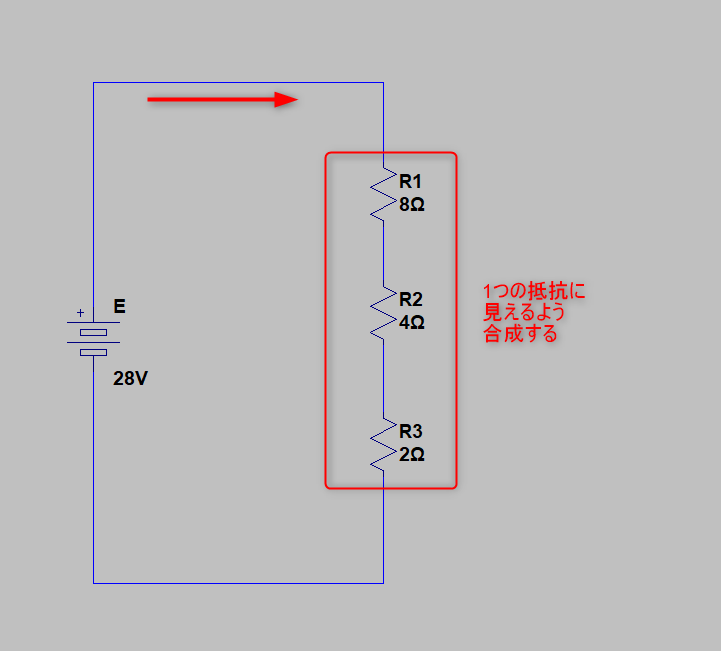
R=8+4+2 =14(Ω)
I=E/R=28/14 =2(A)
ですね
全体の電流がわかれば、直列回路の性質から
I=I1=I2=I3 =2A
です
各抵抗の「電流」がわかれば、「抵抗値」は判りますから
E1,E2,E3を求めることが出来ます
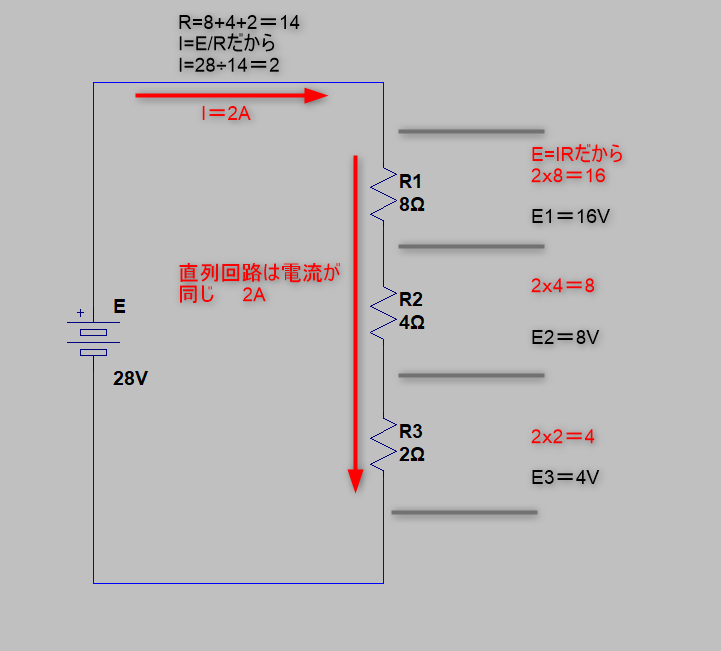
直列接続は「抵抗の比=電圧の比」
また、抵抗の比率に応じた電圧になっています
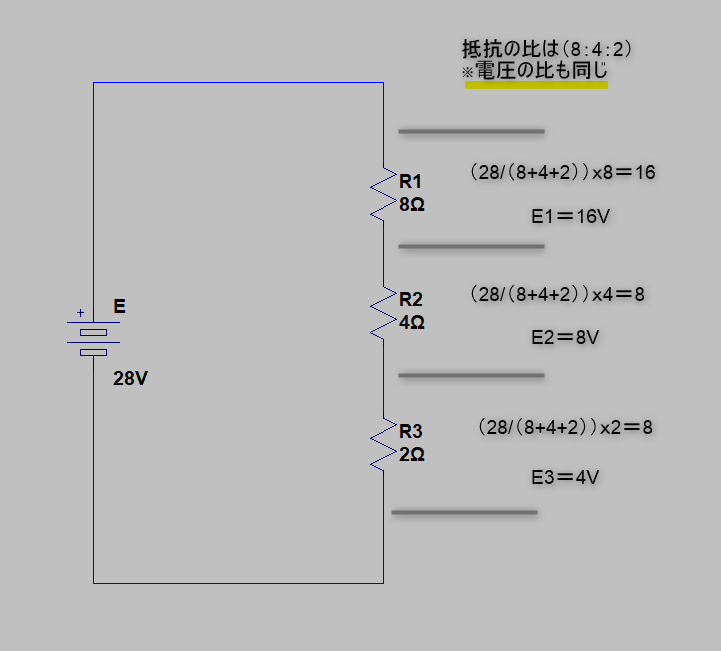
抵抗の直列回路では「抵抗の比」が「電圧の比」になります
R1:R2:R3 = E1:E2:E3
これを応用して、抵抗の電圧を求めることが出来ます
例えば、E1を求めるには
まず、各抵抗の比を求めます
8Ω:4Ω:2Ω
※比率は同じ数を「割る、かける」しても同じです
8:4:2 = 4:2:1 ですね
「比率1当りの電圧」を求め、それに「各比率をかける」
全電圧は E=28V
そして、比率1当たりの電圧は
28÷(4+2+1)=4
求めたい抵抗の比率をかける
E1=4x4=16V
E2=4x2=8V
E3=4x1=4V
※別の求め方
En= (Rn/R ) x E
E1を求めるなら
E1= (R1/R1+R2+R3 ) x E
値を代入してみます
(8÷(8+4+2))x28
=8÷14x28
E1=16V
E2・E3も同様に求めることが出来ます
電卓などが許可されている資格試験などは、コチラでもOKです
抵抗の並列接続
このようなつなぎ方を「並列接続」といいます
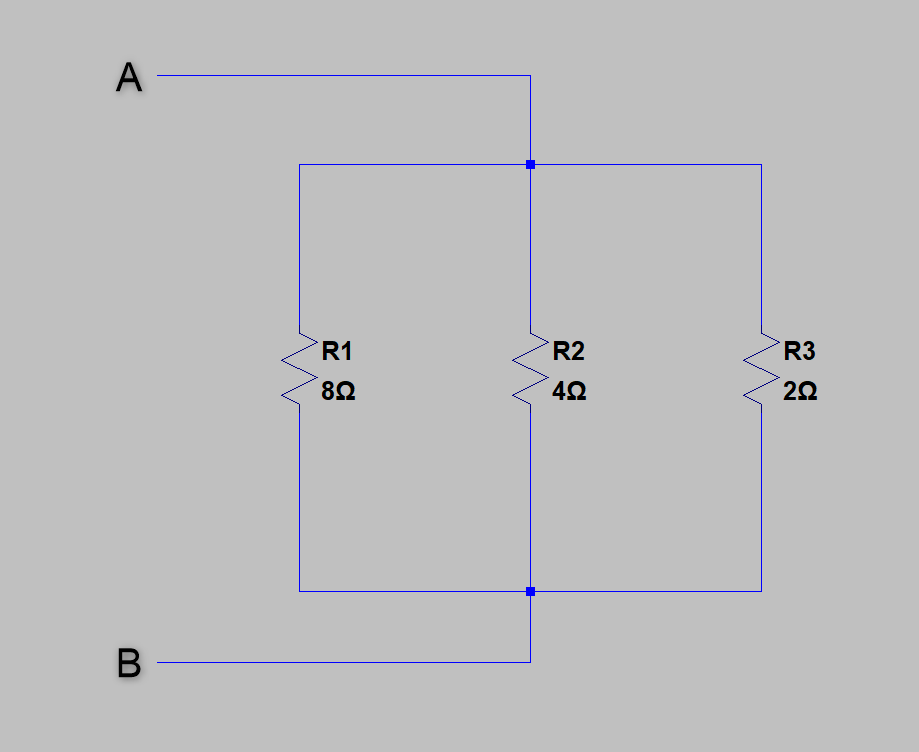
この抵抗の「並列接続」を理解することが、
オーム法則「公式」の「最大の試練」です
A-B間から見ると、電気的に「一つの抵抗」に見えます
A-B間の抵抗値を「R」とすると
1/R= 1/R1 + 1/R2 + 1/R3
または
R=1/(1/R1+1/R2+1/R3)
抵抗がR4、R5・・・と増えても同じように計算します
これは・・・分かりづらいです
上の式は1/Rなので、使う時に間違いやすいですね
下の式は分数だらけで、見るだけでも、「ゾッ」とします
が・・・
実は、ステップに分けて「順序よく計算」すれば、難しいことはないのです
この計算を図で説明してみます
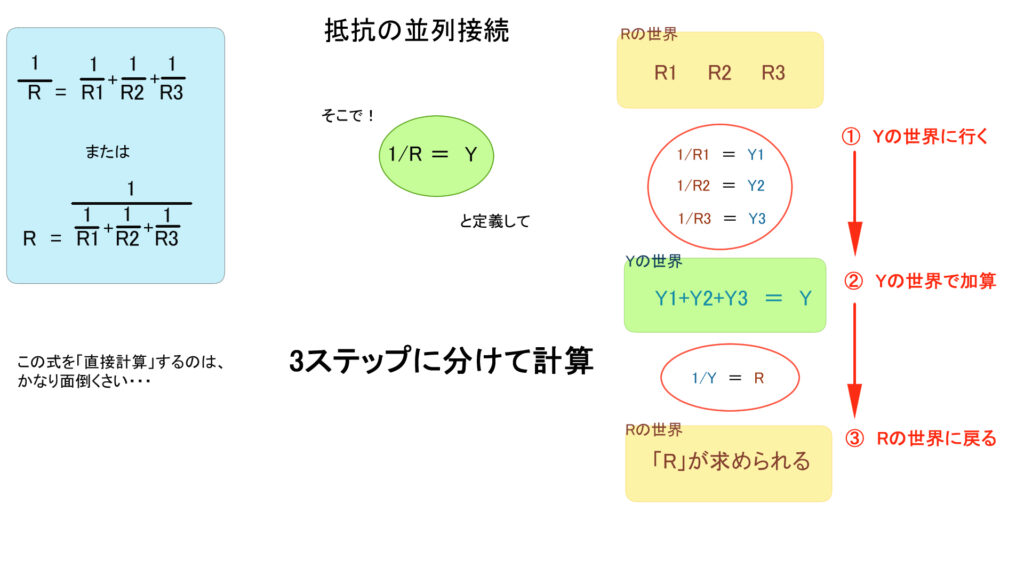
並列接続は「公式と3ステップ計算」両方覚えておくとGOODです
抵抗の並列接続に「特有の性質」も重要です
覚えておきましょう
「並列接続」の各抵抗にかかる「電圧」は
A-B間の「電圧をE」とすれば、
E=E1=E2=E3
各抵抗の「電流」の関係は
- ① I=I1+I2+I3
- ② 各抵抗の電流は「抵抗逆数の比」になる
- これは、1/R1:1/R2:1/R3 = I1:I2:I3
- あるいは、Y1:Y2:Y3 = I1:I2:I3 といえます
抵抗の並列回路を「実際に計算」してみる
この回路で「電流」と「電圧」をそれぞれ計算してみます
この計算では、並列抵抗の「合成抵抗」と「特有の性質」を使っています
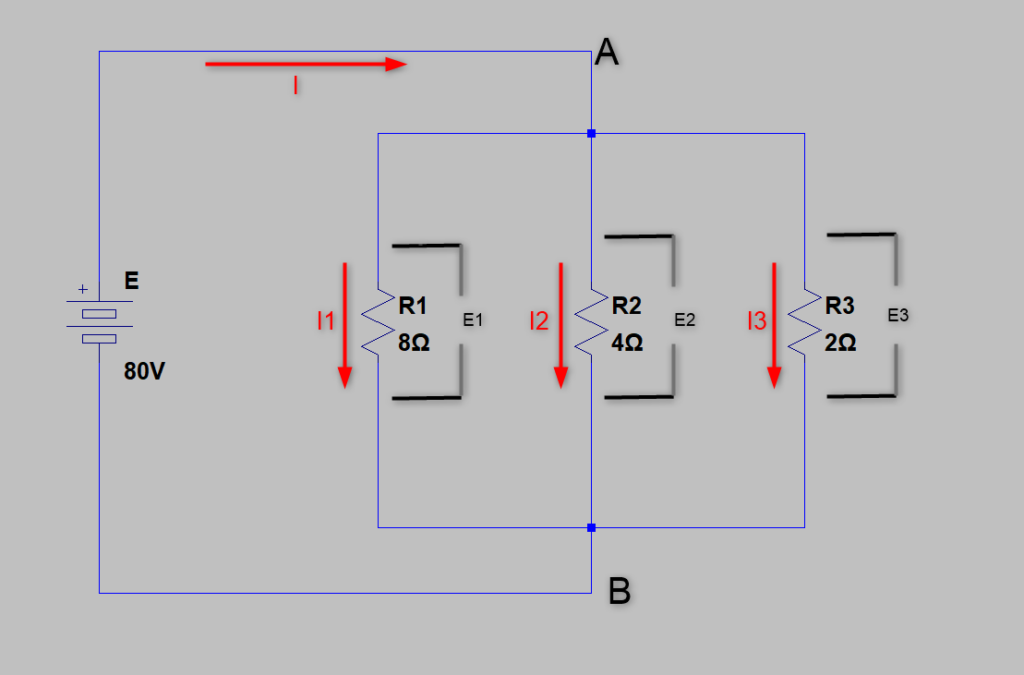
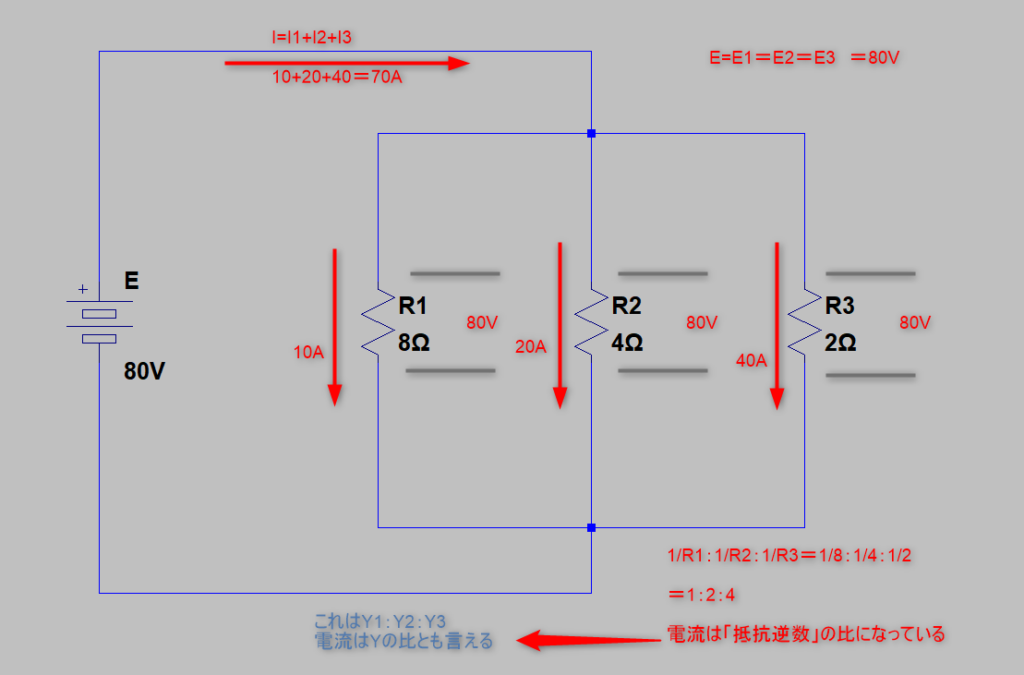
この回路では
E=E1=E2=E3 =80(V)
ですね
各抵抗にかかる電圧が判明したので
I=E/Rより
I1=80/8 =10(A)
I2=80/4 =20(A)
I3=80/2 =40(A)
I=I1+I2+I3
I=10+20+40 =70
I=70(A)
この回路の合成抵抗は、
R=E/I より
80/70 = 8/7(Ω)です
合成抵抗から計算してみる
今度は、正攻法に合成抵抗「R」を求めてから
全電流「I」と各抵抗の電流を求めてみます
抵抗の並列接続「合成抵抗」からアプローチしてみましょう
① Y1=1/8 Y2=1/4 Y3=1/2
② Y=1/8+1/4+1/2
=1/8+2/8+4/8
Y=7/8
③ R=1/Y =8/7(Ω)
合成抵抗Rは8/7(Ω)です
次に電流Iを求めます
I=E/R =80÷(8/7)
=80x(7/8) =560/8 =70
I=70(A)
当然ですが、同じ答えが導かれます
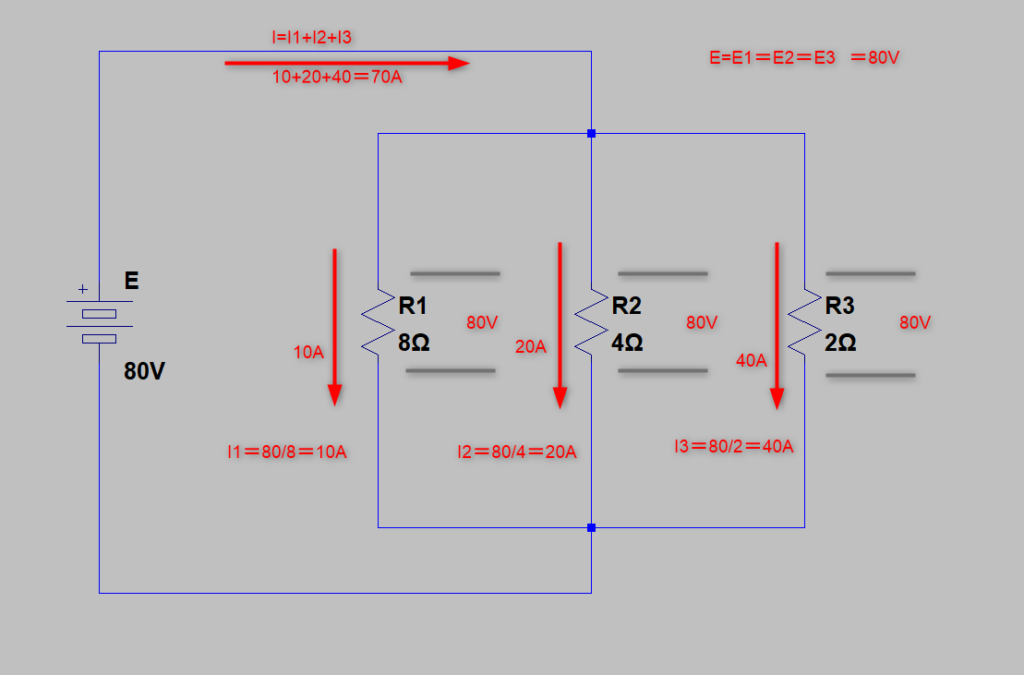
並列接続は「抵抗逆数の比=電流の比」
各電流は抵抗逆数(Y)の比ですから
1/R1:1/R2:1/R3 = 1/8:1/4:1/2
これは、1:2:4 ですね
比率1当たりの電流は
70/(1+2+4) = 10
各比率を代入すると
I1=1x10 =10(A)
I2= 2×10 = 20(A)
I3= 4×10 = 40(A)
※別の求め方としては
In=(Yn/Y)xI
I1を求めるなら
I1=(Y1/Y1+Y2+Y3) xI
値を代入すると
I1=(0.125/0.125+0.25+0.5)x70
=(0.125/0.875)x70
=10
I2・I3も同様に求めることが出来ます
電卓などが許可されている資格試験などは、コチラでもOKです
直列と並列が混ざった回路
「直列と並列が混ざっていない」部分から
合成抵抗を求めていきます
合成抵抗を求める
①最初に計算するのは「R1とR2の並列接続」です
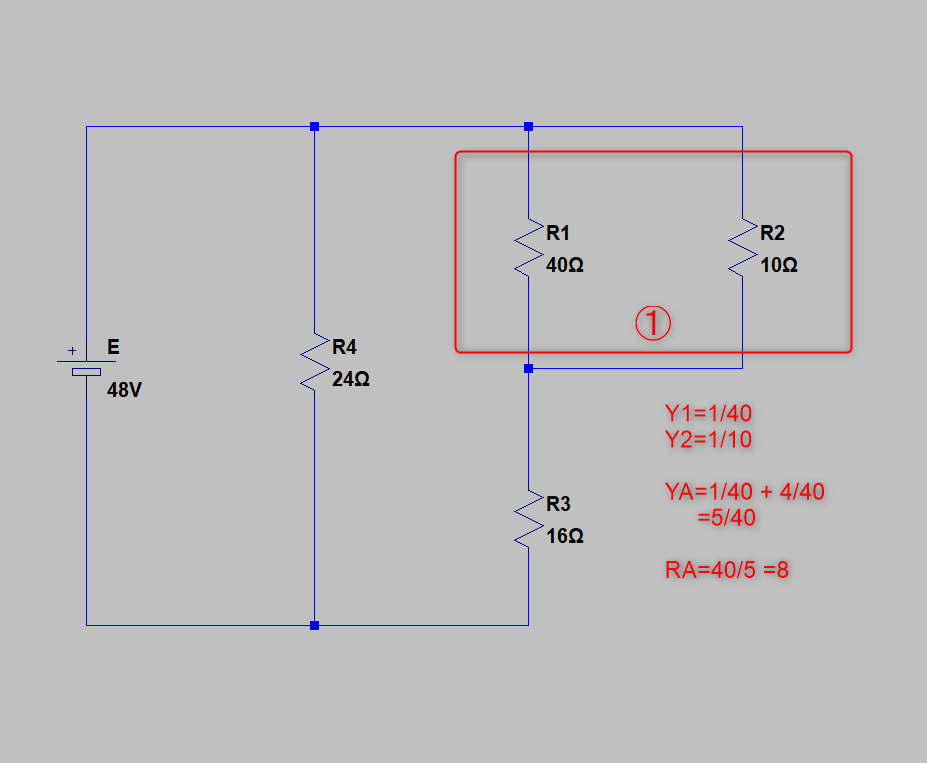
②次は、最初に求めた「RAとR3の直列接続」を求めます
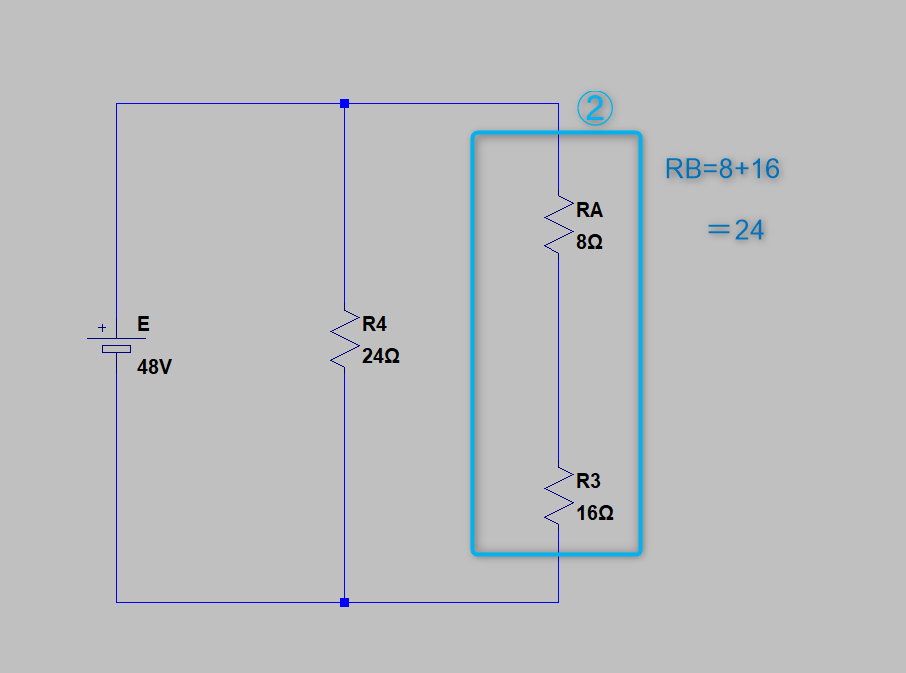
③そして、最後は合成された「RBとR4の並列接続」を求めます
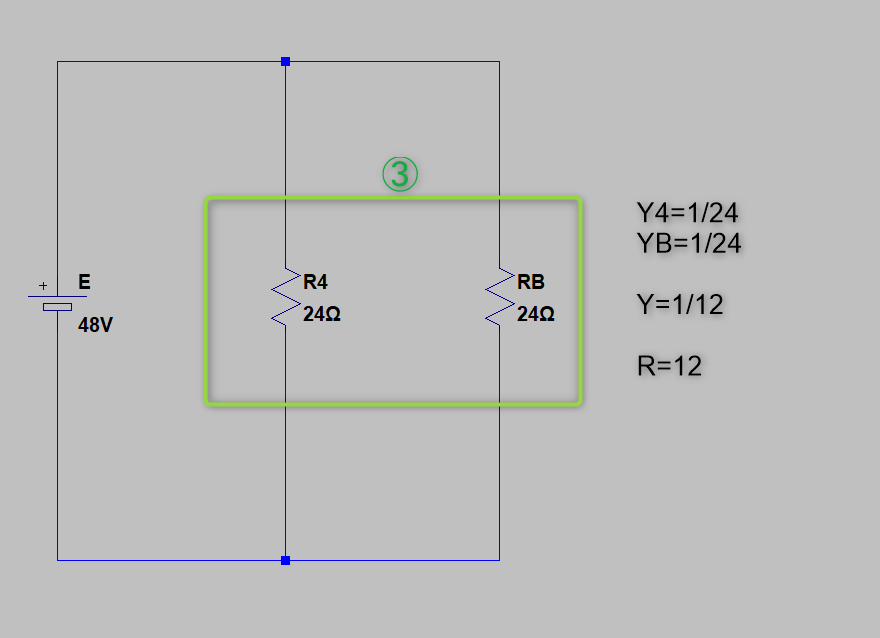
この回路の合成抵抗「R」は12Ωですね
各抵抗の電圧、電流を求める
合成抵抗「R」が計算できれば全電流「I」が計算できますね
48V/12Ω =4A
そして、合成抵抗の計算とは「逆の手順」を使って
今度は「各抵抗の電圧、電流」を求めます
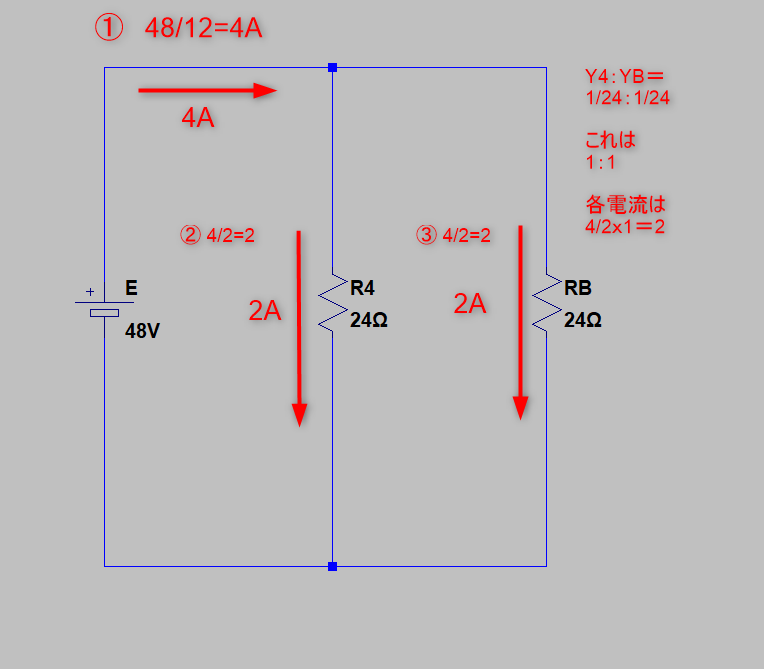
並列の電流は1/Rの比(Yの比)になりますから
I4=2A
IB=2A
となります
次は、RBを一つ前の戻します
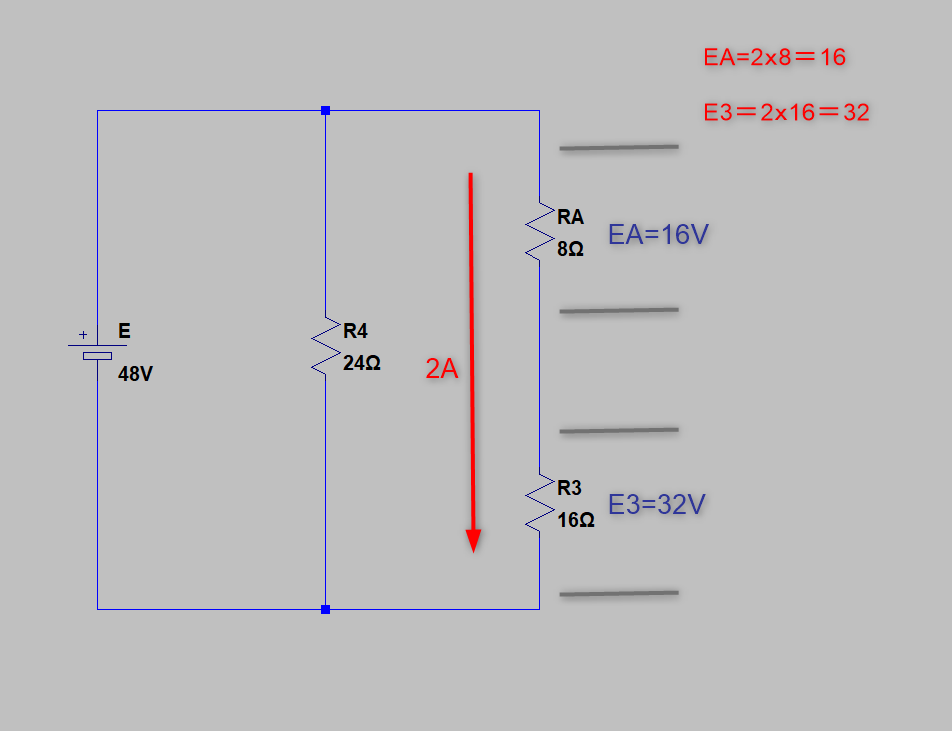
電流がわかりましたので「オームの法則」から電圧が計算できます
EA=16V
E3=32V
ですね
そして、RAを元に戻すと
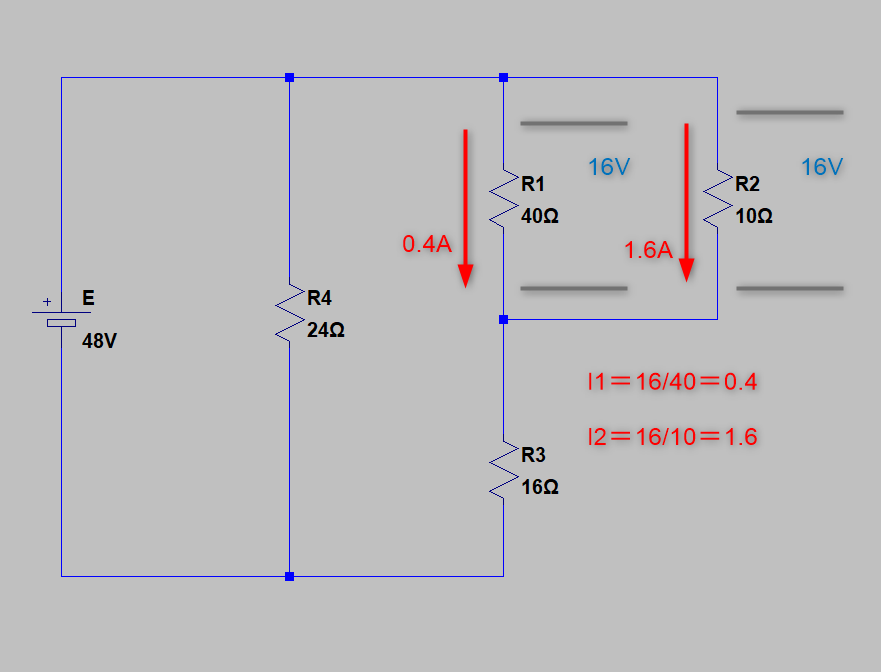
今度は抵抗両端の電圧が判っていますから
I1=0.4A
I2=1.6A
と計算できます
これで、全ての抵抗の電圧と電流が計算できました
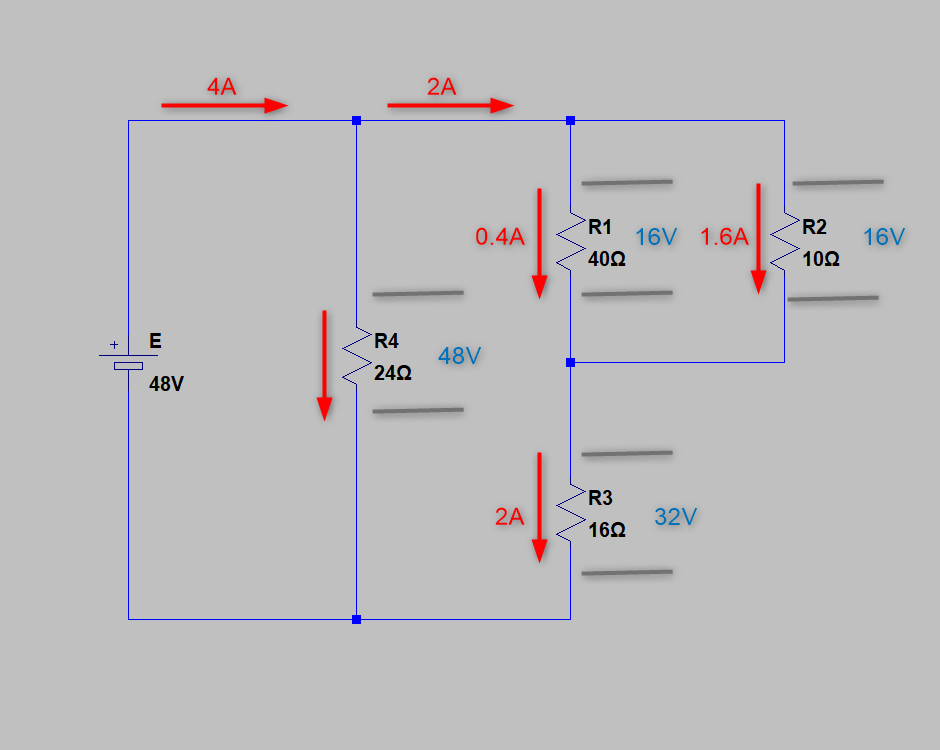
(I4=2A、図に書き忘れです)
まとめ
オームの法則は「電圧・電流・抵抗」の関係を公式にしたものです
電気の世界では、超重要な公式です
①まず、公式を覚えましょう

②オーム法則の公式を使うには
1つの抵抗で「電圧」「電流」「抵抗値」
いずれか2つが判明している必要があります
③複数の抵抗は「抵抗の合成」によって
見かけ上「一つの抵抗」として扱うことができます
④抵抗の接続は「直列接続」と「並列接続」に分かれます
抵抗の直列接続は
- R=R1+R2+R3・・・Rn
- I=I1=I2=I3
- E=E1+E2+E3
- R1:R2:R3= E1:E2:E3
抵抗の並列接続は
- 1/R=1/R1+1/R2+1/R3・・・1/Rn
- E=E1=E2=E3
- I=I1+I2+I3
- 1/R1:1/R2:1/R3= I1:I2:I3
おまけの話
直接来られた方もいらっしゃると思いますが
実は、ここ、電子工作をお題にしたブログです
そこで、ちょっと専門的な話題にも触れたいと思います
興味があれば御覧ください
抵抗の逆数「Y」は実在する?
はい、実在します
一般的には交流的な抵抗(インピーダンス=Z)の逆数で
「アドミタンス」と呼ばれるものです
なんと、単位「S」(ジーメンス)まで持っています
電子回路などでは、真空管(5極管)やFETのパラメーター
「相互コンダクタンス(gm)」の単位として見かけます

余談:昔は「℧」とかいて「モー(mho)」と呼ばれていました
Ωの逆数ですから「記号も読み方」もオーム(ohm)の逆さというわけです
これ・・・マジです

電子工作での「オームの法則」
せっかくなので、電子工作でよく使われるケースを紹介します
①LEDの抵抗
LEDは「発光ダイオード」とも呼ばれる半導体の一種です
LEDの点灯は、いちばん簡単な電子工作です

LEDは電球と違い
電源を直接つなぐと壊れてしまいます
原因は電流の流れすぎです
LEDを点灯させる場合
壊れないように電流を制限する抵抗が必要です
計算などを詳しく知りたい方は、コチラに記事があります

②デジタル回路での出力増強
Arduinoなどの「マイコンボード」は「3.3V」あるいは「5V」で動いています
もっと「高い電圧」や「多くの電流」を制御したい場合
図のように「トランジスタ」などを使うことが一般的です
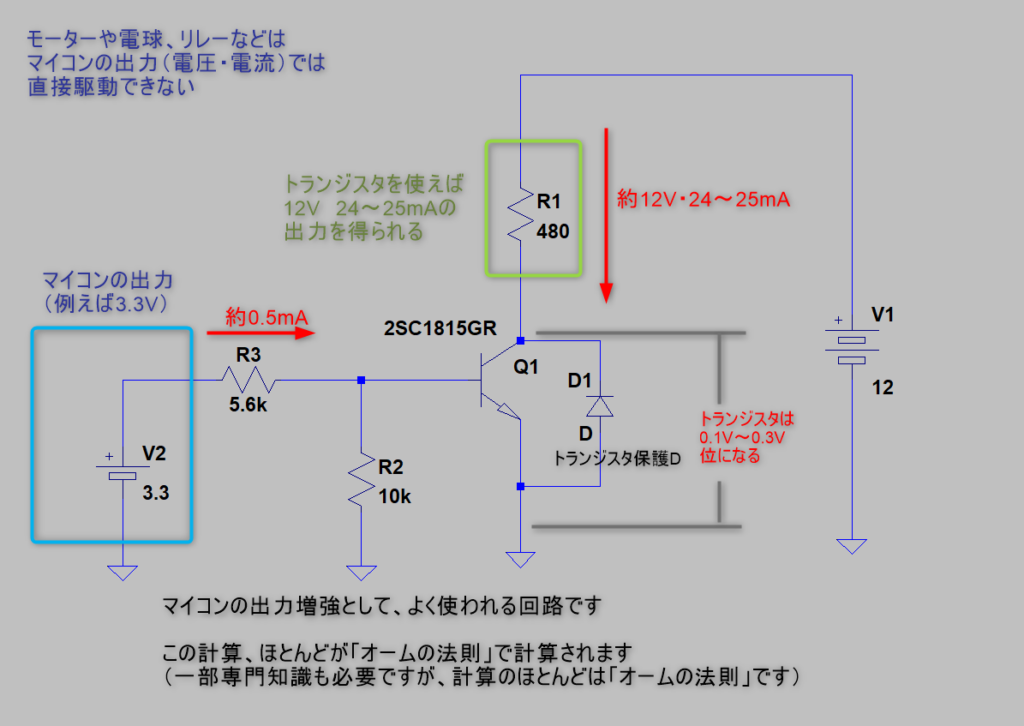
一見、難しそうに見えますが、実は計算の大半が「オームの法則」です
詳しくは、コチラに考え方、設計法を書きました

③アナログ回路のバイアス
基本的なアナログ回路の初段によく見かけます
入力波形がキチンと増幅されるように、少し電圧をかけます(バイアスといいます)
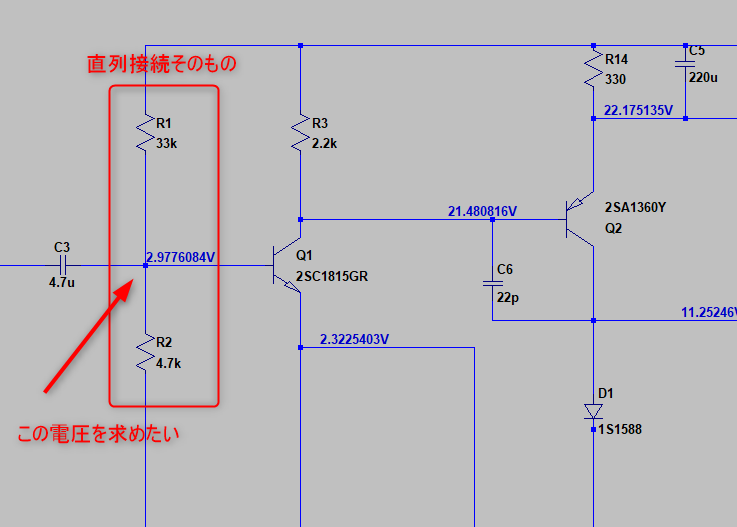
この電圧の計算は、まさに直列接続ですね
R2/(R1+R2)・E
トランジスタと増幅回路は、こちらの記事です

※これらは「一例」です、電子回路の至るところで「オームの法則」が使われています
以上、おまけでした





